Shoot Down an Asteroid

Would it be possible to stop an asteroid from hitting the earth by firing bullets at it? --Myself

I'll be analyzing one of my own thoughts this time. I'm sure literally everyone^[who?] has wondered about this. For the purposes of this post, I'll assume that we're talking about the asteroid 4942 Munroe. It's big enough to be interesting (6 to 10 kilometers across[1], so I'll go with 8 kilometers), but not big enough to actually destroy the earth. Asteroids typically travel at 25 kilometers per second.[2] Asteroid densities vary widely[3], but let's assume that 4942 Munroe has a density of 4 grams per cubic centimeter. From this, I can calculate that the momentum of 4942 Munroe is 1.28*10^19 kilogram-meters per second.

Now it's time to think about the guns. An AK-47 fires 600 rounds per minute at a velocity of 715 meters per second.[4] Each round weighs 7.9 grams.[5] If one AK-47 is fired straight at the asteroid, the asteroid will lose 715*0.0079*600=3,389.1 kilogram-meters per second every minute. At this rate it would take slightly over 7 billion years to bring 4942 Munroe to a halt. Chances are that there will be no earth to hit by then anyway.

Luckily for humanity, it's possible to do better, but it'll take some thinking. The ideal gun for this sort of task would have massive bullets with high velocity and a high rate of fire. The heavy artillery of World War I and World War II had massive ammunition and often that ammunition had a high velocity. The railway gun Krupp K5 had a shell mass of 255 kilograms and a muzzle velocity of 1120 meters per second. The low firing rate (0.25 rounds per minute) might be a problem, but let's see. 1120*255*0.25=71,400 kilogram-meters per second lost per minute. This would bring the time down to 341 million years, which is actually a lot better than the AK47 (but still impractical). Some cannons are better. The immense V-3 cannon has a far higher rate of fire and muzzle velocity, but only a slightly lower shell size. A V-3 cannon being fired at the asteroid would cause it to lose momentum at a rate of 1,050,000 kilogram-meters per minute, which brings the time down to under 24 million years. The anti-aircraft gun GAU-8 Avenger (link to WP) is slightly superior (13 million years). None of these are going to cut it though.

More modern weapons can do still better. Consider railguns, which are moving from experimental devices into ones with practical uses. The US Navy plans in 2016 to test a railgun with a firing rate of 10 rounds per minute, a muzzle velocity of 2500 meters per second, and a bullet mass of 10.5 kilograms[6] Even that is not enough: the stopping time would be nearly 100 million years. The last thing that I'll try is this Assuming a muzzle velocity of 1000 meters per second, it would take 2.4 million years for one of those to stop 4942 Munroe. Giving one to every person on earth would stop the asteroid in just under three hours, but that wouldn't be practical.

I guess we're doomed if a huge asteroid comes our way. Or not?

Freefall

If you jumped into a hole in the center of the earth, how long would it take to come to a stop? --Sodium

I feel compelled to explain why this is not entirely practical. For one thing, it's entirely likely that such a hole would collapse, but let's assume it's lined with a magic extra-strong material that also keeps the tunnel from reaching temperatures of thousands of degrees. The air pressure would also be a problem. We currently have only 62 miles (100 kilometers) of air above our heads, so having several thousand miles of air about our heads would likely crush us.

With that out of the way, let's turn to the actual scenario. I'll assume that this tunnel is a vacuum (so that the air pressure doesn't crush the jumper [and because physicists like working in a vacuum]) and that it's sealed at both ends (so the tunnel isn't filled with wind). I'll also assume that your aim is good enough that you don't hit any walls, which would (obviously) kill you.

The exact formula for figuring this out is more complicated than traditional gravitational acceleration since the mass that's actually pulling on you will decrease as you approach the center of the earth.[1] On average, the jumper's acceleration will be about 5 meters per second squared, but it does change some.[2] I'll assume that the change in acceleration (jerk) is constant, even though it isn't, to simplify the equations. Because I'm lazy!

I can't resist going off-topic to describe some rather interesting facts. As everyone (who's read this far at least) knows that velocity, acceleration, and jerk are the 1st, 2nd, and 3rd derivatives of motion. What you may not know is that jounce (or snap), crackle, pop, lock, drop, shot, and put are the 4th, 5th, 6th, 7th, 8th, 9th, and 10th derivatives of motion, respectively. Just an awesome fact that was worth sharing. I don't know why anyone would use these though.

Anyway, back to business. I wrote a bit of code which tells me the average jerk and also tells me that it would take about 22 minutes to fall to the center of the earth. This implies that it would take 21 minutes, so my math can't be that far off. It doesn't really matter though, since your momentum would carry you all the way back up to the surface, at which point you'd just repeat it all over again.[3]

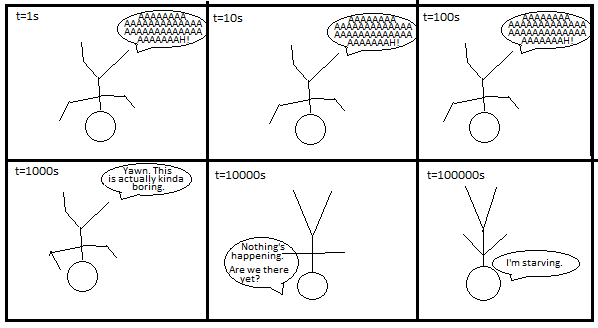
I wonder how long it would take for a person to get bored of falling assuming they didn't know that they'd never hit the ground...

Apologies

I just want to apologize for the long delay with no posts. I have been busy with other things lately, but I will try to make a new post soon. Thanks,

--Jakob